The price of morality

What would happen to prices if firms started internalizing the social impact of their behavior?

What would happen to prices if firms started internalizing the social impact of their behavior? A few years ago I published a model of moral management in competitive markets (Martin 2019) and I thought it would be an interesting exercise to take the price and quantity functions from this model to make a price index. This is my first attempt to take a model where firms are not price takers and consumers aren’t standard utility maximizers and derive a price index as a function of how some deeper parameter changes over time.

The model

The model has two identical firms selling differentiated products to socially-conscientious consumers with heterogeneous preferences. Firms are able to engage in socially responsible behavior (e.g., voluntarily abating harmful emissions), with the twist that their motivation for doing so can be both for the usual strategic reasons and due to the preferences of the firm’s management—a moral manager. A greater degree of moral management means that a firm places more weight on pro-social behavior relative to profit, whereas a profit-maximizing manager places no weight on pro-social behavior and only considers profit. An increase in the degree of moral management for a firm affects the amount of pro-social behavior by both firms in the market, and consequently affects prices and expenditure/revenue shares for both products.

Part of the solution for the model is a pair of price and quantity functions that give the prices and market shares as a function of the degree of morality for each firm’s manager. These can be plugged into a price index to give a measure of the change in price from a change in managers’ preferences over time. In particular, comparing prices when managers are profit maximizers to prices with moral managers give a measure of the change in price due to moral managers.

Impact of morality on price

Let’s start with the simplest case: the two firms each have the same type of manager. In this case prices will be the same for both firms’ outputs (which do not change over time), so any price index that satisfies the proportionality axiom will simply be the change in price over time. Equations (2) and (3) in the paper can be used to establish that this change in price over time is a linear function of the degree to which managers value the social impact of their firm’s behavior, \(1 + \alpha \mu\), where \(\alpha\) is a complex function of the parameters of the model and \(\mu\) is the degree to which the manager values the social conduct of the their firm (relative to profits). Therefore, an increase in the morality of managers in the market will translate into an increase in any reasonable price index over time.

The more interesting case is when firms have different types of managers. In this case, an increase in the morality of one firm’s management will lead to an increase in price and quantity for that firm’s product and a (smaller) decrease in price and quantity for the competitor’s product. The increase in price for one product and decrease in price for the other work against each other to dampen the increase in price when firms are run by the same type of manager. Note that the expenditure/revenue share increases for the product with the increasing price, the opposite of what’s usually expected, and this means that the Paasche index is larger than the Laspeyres index.

Rather than try to get a closed-form expression for a price index as a function of the degree of moral management in the market, let’s work through some numerical examples to see how it compares to the case when both managers have the same type. We’ll start by making a class to generate price relatives and expenditure shares for a pair of types, relative to profit-maximizing managers.

import pandas as pd
import numpy as np
from typing import Callable


class ConstraintError(Exception):
    pass


class MoralManagers:
    def __init__(self, t: float, v: float, c: float, k: float, F: float) -> None:
        t = float(t)
        v = float(v)
        c = float(c)
        k = float(k)
        F = float(F)
        if t <= (v - k) ** 2 / (3 * F):
            raise ConstraintError("t is too small")

        self.phi = (9 * t * F - (v - k) ** 2) / (9 * t * F - 2 * (v - k) ** 2)
        self.rho = (v - k) ** 2 / (9 * t * F - (v - k) ** 2)
        self.t = t
        self.v = v
        self.c = c
        self.k = k
        self.F = F

        base_s = (self.v - self.k) / (3 * self.F)
        self.base_p = self.p0(base_s, base_s)

    def p0(self, s0: float, s1: float) -> float:
        return (
            self.t
            + self.c
            + (self.v + 2 * self.k) / 3 * s0
            - (self.v - self.k) / 3 * s1
        )

    def p1(self, s0: float, s1: float) -> float:
        return self.p0(s1, s0)

    def q0(self, p0: float, p1: float, s0: float, s1: float) -> float:
        return 0.5 + (self.v * (s0 - s1) - p0 + p1) / (2 * self.t)

    def q1(self, p0: float, p1: float, s0: float, s1: float) -> float:
        return self.q0(p1, p0, s1, s0)

    def s0(self, mu0: float, mu1: float) -> float:
        return (self.v - self.k) / (3 * self.F) + self.phi / self.F * (
            mu0 - self.rho * mu1
        )

    def s1(self, mu0: float, mu1: float) -> float:
        return self.s0(mu1, mu0)

    def pi(self, p: float, q: float, s: float) -> float:
        return (p - self.c - self.k * s) * q - self.F / 2 * s**2

    def pqs(self, mu0: float, mu1: float) -> dict:
        s0 = self.s0(mu0, mu1)
        s1 = self.s1(mu0, mu1)
        p0 = self.p0(s0, s1)
        p1 = self.p1(s0, s1)
        q0 = self.q0(p0, p1, s0, s1)
        q1 = self.q1(p0, p1, s0, s1)
        pi0 = self.pi(p0, q0, s0)
        pi1 = self.pi(p1, q1, s1)
        share0 = p0 * q0 / (p0 * q0 + p1 * q1)
        if pi0 < 0:
            raise ConstraintError("negative profit for firm 0")
        elif pi1 < 0:
            raise ConstraintError("negative profit for firm 1")
        else:
            return {
                "rel0": p0 / self.base_p,
                "rel1": p1 / self.base_p,
                "share0": share0,
            }


def laspeyres_index(rel0: float, rel1: float, share0: float) -> float:
    return rel0 * 0.5 + rel1 * 0.5


def paasche_index(rel0: float, rel1: float, share0: float) -> float:
    return 1 / (share0 / rel0 + (1 - share0) / rel1)


def fisher_index(rel0: float, rel1: float, share0: float) -> float:
    return (laspeyres_index(rel0, rel1, share0) * paasche_index(rel0, rel1, share0))**0.5


def tornqvist_index(rel0: float, rel1: float, share0: float) -> float:
    return rel0 ** (0.5 * 0.5 + 0.5 * share0) * rel1 ** (0.5 * 0.5 + 0.5 * (1 - share0))


def make_index(data: pd.DataFrame, index: Callable) -> pd.Series:
    return data.apply(lambda x: index(x["rel0"], x["rel1"], x["share0"]), axis=1)

We can now simulate the impact of an increase in morality for one firm on a Fisher index under three scenarios: managers are entirely uncorrelated, so that the other firm is always a profit maximizes; managers are somewhat correlated; and managers are perfectly correlated and have the same type. In order to respect the constraint that firms must make positive profit, we’ll only consider a change in morality up to the point at which the manager places equal value on profitability and social conduct.

def simulate(corr: float, model: MoralManagers) -> pd.DataFrame:
    df = [
        pd.DataFrame(model.pqs(m, corr * m), index=[m]) for m in np.arange(0, 1.05, 0.05)
    ]
    return pd.concat(df)


mm = MoralManagers(3, 2, 0.25, 0.25, 1)

simulation = {corr: simulate(corr, mm) for corr in [0, 0.5, 1]}

fisher = pd.concat(
    {f"corr={corr}": make_index(s, fisher_index) for corr, s in simulation.items()},
    axis=1,
)
fisher.plot(ylabel="Fisher index", xlabel="Degree of morality")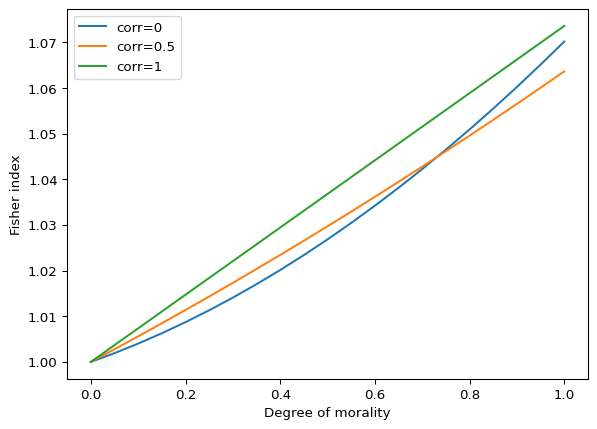

The top line shows the linear effect of morality on price when both firms have the same type of manager. Introducing heterogeneity in the types of managers results in a smaller increase in price, although the Fisher index is now a convex function of the degree of morality, with the curvature becoming more pronounced as managers’ types become less correlated. This is driven by the Paasche index, as the Laspeyres index is a linear function of the degree of morality.

df = pd.DataFrame(
    {
        "Laspeyres index": make_index(simulation[0], laspeyres_index),
        "Paasche index": make_index(simulation[0], paasche_index),
    }
)

df.plot(ylabel="Index", xlabel="Degree of morality")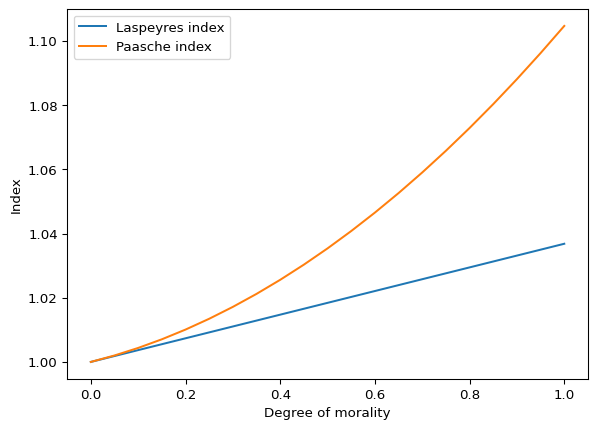

Using a Törnqvist index instead of a Fisher index gives the same general result.

tornqvist = pd.concat(
    {f"corr={corr}": make_index(s, tornqvist_index) for corr, s in simulation.items()},
    axis=1,
)
tornqvist.plot(ylabel="Törnqvist index", xlabel="Degree of morality")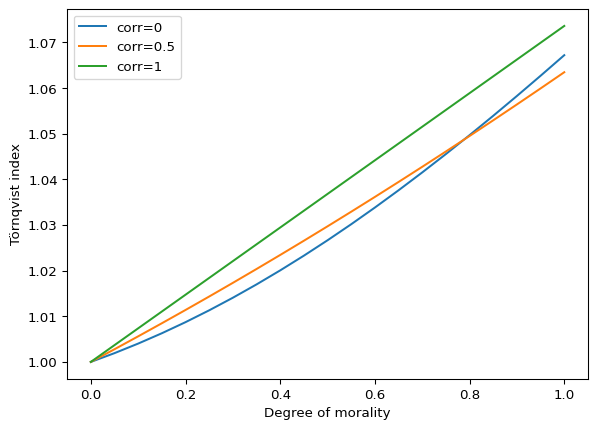

I find this to be an interesting result. Despite coming from a model in which both firms and consumers are making optimal decisions, an increase in the degree of morality from one firm in the market results in price indexes that behave quite differently than expected.

References

Martin, Steve. 2019. “Moral Management in Competitive Markets.” Journal of Economics & Management Strategy 28 (3): 541–60. https://doi.org/10.1111/jems.12283.